据能源圈了解到，

摘要：锂离子电池的电化学阻抗谱包含了丰富的电池内部信息，相较于常用的电流、电压和温度等电池参数具有更大的应用潜力。因此，提出了一种基于电化学阻抗谱对电池的荷电状态进行估计的方法。首先，通过实验并借助更具实用价值的阻抗测量板获得了三元锂电池在不同荷电状态下的阻抗数据；其次，在现有锂离子电池等效电路模型的基础上，提出了新的拟合精度更高的等效电路模型；最后，利用电池的阻抗谱数据对提出的等效电路模型进行参数辨识，从中找到了与电池荷电状态高度相关的参数，成功实现了对其荷电状态的准确估计。

关键词：电化学阻抗谱；等效电路模型；荷电状态估计；阻抗测量板

准确地预测出锂离子电池的荷电状态(state of charge, SOC)，可以更好地评估电池的可用能量和剩余使用时间，避免电池过充和过放，以及优化系统与能量管理策略，对于整车的安全性、可靠性具有重要意义。但是由于电池的充放电过程是一种多因素相互耦合的复杂非线性过程，而这些影响因素对电池的确切作用很难从常规的电流、电压以及温度等参数当中识别到，所以实现对锂离子电池SOC的准确估计到目前为止仍然是一个难题。

作为一种经典的电化学系统测试方法，通过在电池上施加一个小的电流扰动，然后测量电池的电压响应就可以得到电池的电化学阻抗谱(electrochemical impedance spectroscopy, EIS)。锂离子电池的EIS能够无损检测锂离子电池的内部特征，不仅包含了丰富的电池内部信息，同时也不易受外界环境的影响，相较于其他电池参数具有更好的稳定性和可靠性[1]。但是实际应用时存在电池EIS数据获取难度大的问题。因此本文提出了一种基于具有应用潜力的阻抗测量板测得锂离子电池EIS数据对其SOC进行估计的方法，旨在充分利用锂离子电池的电化学阻抗谱的数据实现对其SOC的准确估计，以保障电池系统高效、安全、稳定的运行，并为电池SOC的估计提供一种新的途径。

1 研究背景

到目前为止，有许多学者对基于EIS数据估计锂离子电池SOC的方法都进行了研究。总的来说，就是从EIS数据中提取和SOC相关的特征并利用这些特征对SOC进行估计。根据从EIS数据当中提取特征的方式不同研究大致可以分为两种。一种是直接使用原始的EIS数据，如阻抗幅值、相位以及某一频率下的特定阻抗等作为特征对电池SOC进行估计。戴海波等发现在温度一定时，0.1 Hz下的阻抗相位绝对值随电池SOC的增大而单调递减，并用线性函数拟合了不同温度下两者的关系，实现了在温度已知时基于EIS对电池SOC估计的方法[2]。Kong等则通过计算不同频率下的阻抗实部及虚部数据和电池SOC之间的各种相关系数，找出了八个和SOC之间高度相关的阻抗实部或虚部值并建立它们和SOC之间的映射关系[3]。另一种则是通过建立电池模型，并利用EIS数据对电池模型进行参数辨识，将辨识出来的参数作为特征来对电池的SOC进行估计。由于多了一个提取特征的步骤，所以可以从电池的EIS数据中挖掘出更多隐含的相关信息来对SOC进行估计。Wang等通过建立一个具有SOC效应的多项式等效电路模型(equivalent circuit model, ECM)，并将该模型用于拟合不同SOC下的EIS数据得到了电池SOC和模型参数之间的非线性关系，实现了通过EIS数据对电池SOC的估计[4]。李植通过建立阻抗模型进行参数辨识，发现电荷转移电阻和电池SOC的关系高度相关，并据此建立了两者之间的多项式关系，实现了对电池SOC的估计[5]。吴忠信则基于稀疏的电池阻抗数据进行分析，研究了所建立的ECM参数与SOC之间的关系，最终确定了以ECM中常相位角元件的参数Y0来对SOC进行估计的思路，并通过分段拟合的方法建立了两者之间的函数关系，实现了使用稀疏的EIS数据对电池SOC进行估计的目标[6]。

上面所列举的基于EIS数据的锂离子电池SOC估计方法都取得了不错的效果，但是他们使用的都是通过电化学工作站获得的阻抗数据，这种数据获取方式成本高，难度大，很难实际应用。为了解决这一问题，在本文中提出了一个基于电池EIS数据和ECM的SOC估计方法。该方法使用一块阻抗测量板获取电池EIS数据，相较于电化学工作站，该阻抗测量板由于体积小，成本低更具实用价值。

2 实验

实验中所使用的设备分为充放电设备以及EIS测量设备两个部分。其中充放电设备由充放电机和上位机组成，如图1所示。通过上位机即可控制充放电机按照指定方式对电池进行充放电。实验所使用的EIS测量设备由主板（红色）、从板（蓝色）以及上位机三部分组成，由大唐恩智浦公司开发，如图2所示。蓝色从板的作用是安装电池，并在阻抗测量芯片的控制下对电池进行激励并采集其响应信号。红色主板的作用则是对从板激励信号和响应信号进行处理得到需要的阻抗数据并发给上位机供使用者分析与存储。同时在上位机中还可以设置从板的激励频带以获得电池在指定频率下的EIS数据。在实验中设定激励信号频率范围为0.015～1 500 Hz。实验所使用的电池为四颗松下NCR18650B三元锂离子电池，其正极材料为镍锰钴氧化物（NMC），负极材料为石墨，文中分别命名为BAT1～4。电池的截止电压上下限分别为4.2和3.0 V，据此进行定容实验，可以得到四颗电池的容量均约为3 000 mAh。

图1 充放电实验设备

图2 EIS测量设备

在实际的应用场景当中，用户更加关注电池在放电时的SOC，并且电池放电一般不会低于20% SOC。所以通过实验获得了四颗电池在放电时从100% SOC到20% SOC，每隔10% SOC，用阻抗测量板测得EIS数据。表1中列出了具体的实验步骤，按照表1中的步骤进行实验，可以得到BAT1在放电过程中不同SOC下的EIS数据如图3中所示。从图中可以看到，在不同的SOC下，通过阻抗测量板测得的电池EIS数据有所不同，整体表现出随着SOC的增加向右移动的趋势。具体来说，在拐点前电池的EIS曲线随着SOC的增加整体表现出右上方移动的趋势。而在拐点之后，代表锂离子在电解液中扩散过程的低频直线则随着SOC的增加整体向左上方移动。

表1 实验步骤

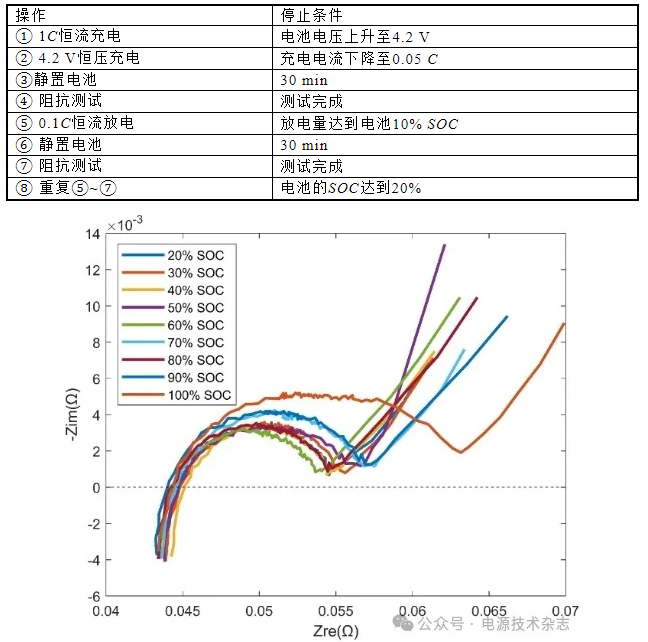
图3 BAT1放电过程中在20%～100% SOC段下的EIS数据

3 建立等效电路模型

通过研究锂离子电池的内部结构和反应过程可以构建出对应的ECM对其进行模拟。例如电池内部的SEI膜通常可以用一个电阻和一个电容或恒相位元件并联进行表示，锂离子在受到低频激励时在电解液当中的扩散过程可以用Warburg阻抗表示等等[7]。相应地，在锂离子电池充放电过程中发生在锂离子电池内部的物理化学反应及其内部的变化也可以被ECM的参数变化所反映，使得利用ECM的参数对电池的SOC估计具有可行性。

图4中列出了一些常用的ECM，为了验证这些模型的拟合精度，使用这些模型对BAT1的EIS数据进行拟合，可以得到拟合的误差如表2所示。误差指标的定义为：

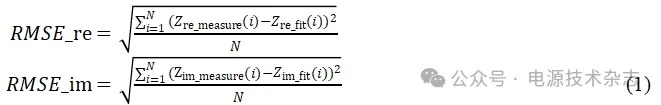
式中：Zre_measure、Zim_measure为实验获得的EIS数据的实部与虚部；Zre_fit、Zim_fit则为通过模型拟合得到的EIS数据的实部与虚部；N为数据数量。从表2中可以看到，使用模型(b)对BAT1的EIS数据拟合时误差最小。这主要是因为使用恒相位元件(constant phase element, CPE)代替模型中的电容能够更好地反应电池内部的反应机理。

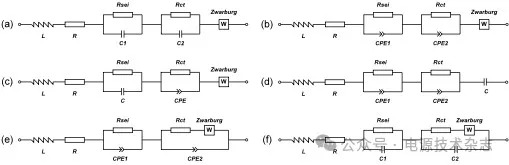
图4 常见等效电路模型

表2 常用等效电路模型的拟合误差

为了直观观察模型(b)的拟合效果，使用该模型对BAT1在90% SOC下的EIS数据进行拟合。拟合结果如图5所示。从图5中可以看到，虽然使用了拟合误差最小的模型，但是拟合结果仍然存在一定的问题，在EIS曲线拐点附近出现了明显的偏离现象，所以如果想要进一步提升拟合效果，需要针对这一方面对模型进行改进。图中模型的拟合误差主要集中在EIS图的低频部分，这一部分表示锂离子在电解液中的扩散过程，在ECM当中通常会使用Warburg阻抗对其进行模拟，但是上面的结果表明单独一个Warburg阻抗很难完全描述电池在受到外部低频激励时内部发生的变化，所以可以尝试在ECM中增加等效电路元件来改善低频时的拟合效果。

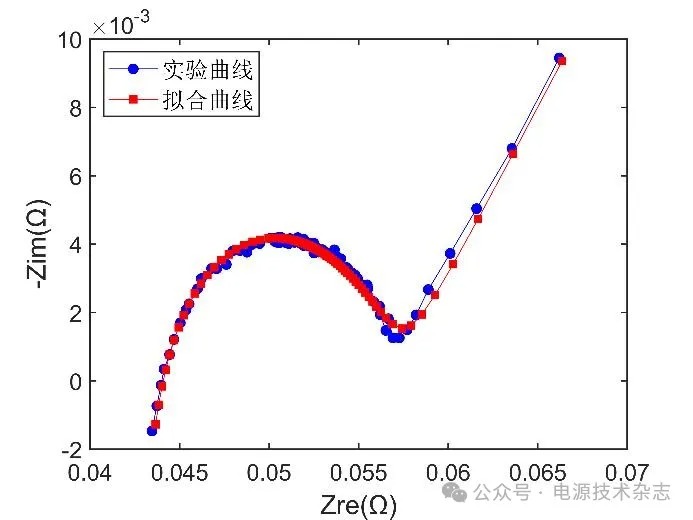
图5 模型(b)对BAT1在90% SOC下的EIS数据拟合效果

图6描述了在受到外部低频激励时锂离子电池内部的反应过程。如图6(a)所示，在受到低频外部激励时，由于一个激励周期的持续时间T较长，电池在此时就像是正在充电和放电，我们把这种状态叫做激励充电和激励放电。假设图6(b)中的电池正处在激励充电状态下，由于持续时间较长，负极附近的电解液中的锂离子数量不足以支撑长时间的电极反应，所以必须有额外的锂离子来源。此时正极处的钴酸锂分解产生锂离子与电子，产生的电子沿着外部导线去往负极，而形成的锂离子则在浓度差的作用下向着负极扩散。但是由于电子移动的速度v2要远大于锂离子在电解液中扩散的速度v1，所以会有部分锂离子聚集在正极处，同时会有部分未在正极参与反应的电子聚集在负极处，正如同图6(b)中红色矩形虚线所圈起来的那样。这个现象和锂离子电池在受到高频激励时在固体电解质界面(solid electrolyte interface, SEI)膜两侧出现的电荷聚集现象十分类似，被叫做双电层[8]。在ECM当中，为了模拟SEI膜的这种双电层效应，通常会在电阻上并联一个电容或恒相位元件，所以在这里同样也考虑在Warburg阻抗上并联一个电容来对锂离子电池受到低频激励时所表现出来的类似现象进行模拟。据此最终构建了图7所示的ECM模型，为了降低模型的复杂度，在模型中将其中的一个恒相位元件替换为了纯电容并最终得到了本文所使用的ECM[9]。为了验证所提出的ECM的有效性，同样使用其对BAT1在90% SOC下的EIS数据进行拟合，如图8所示。从图中可以看到，使用改进后的模型可以很好地改善在低频区域对EIS数据拟合误差较大的问题。

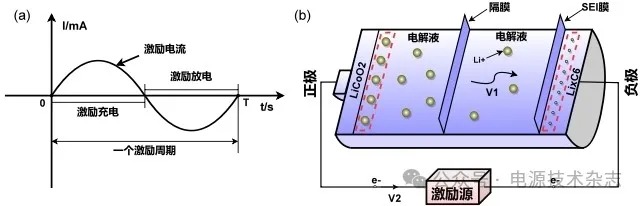
图6 (a)电池在一个激励周期中所处的状态 (b)锂离子电池在受到外部低频激励时内部反应过程

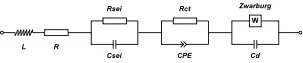
图7 改进后的等效电路模型

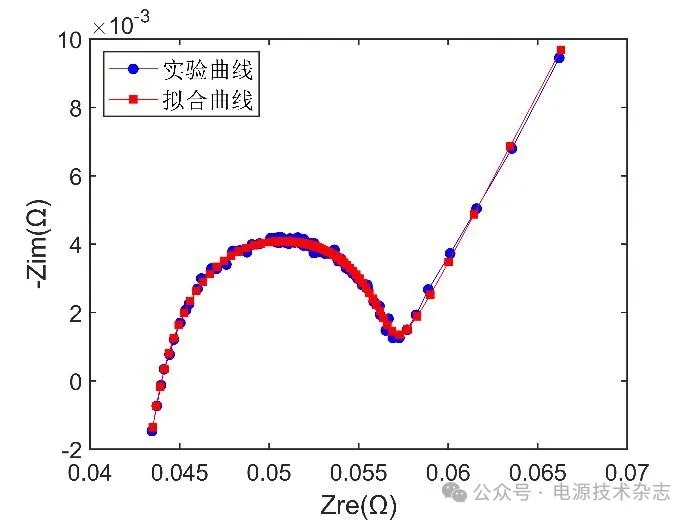
图8 改进后模型对BAT1在90% SOC下的EIS数据拟合效果

4 SOC估计方法

4.1 元件参数随SOC变化趋势

使用图7中的改进ECM对实验数据进行拟合，可以得到ECM参数随电池SOC的变化趋势如图9所示。从图9中可以看到，随着电池SOC的变化，等效电路的元件参数也随之发生了变化。其中恒相位元件的参数CPE-n随电池SOC的变化趋势在四个电池上表现出了较为统一的变化规律。随着电池SOC的增加，CPE-n先增大后减小。这是因为这个参数在一定程度上可以反应电池内部的非线性程度，而电池内部的非线性程度是随着电池SOC的变化而变化的。当电池的SOC较低时，电池的非线性程度较低。这是因为在放电过程中，电池的电荷状态接近空载状态，此时电荷传输过程中的非线性效应较小，电压-电荷关系相对线性。而从低SOC到中SOC（通常是30%～70%之间）段，随着电池SOC的增加，电池的非线性程度会逐渐增加直至最高。这是因为在这个SOC范围内，电池内部的电荷传输、离子扩散和电极反应等过程之间的相互作用会随着SOC增加而逐渐增强，导致电池的电压-电荷关系表现出的非线性特征越来越强。而当SOC继续增加时，电池的非线性程度会再次降低。因此可以利用CPE-n来对电池的SOC进行估计。

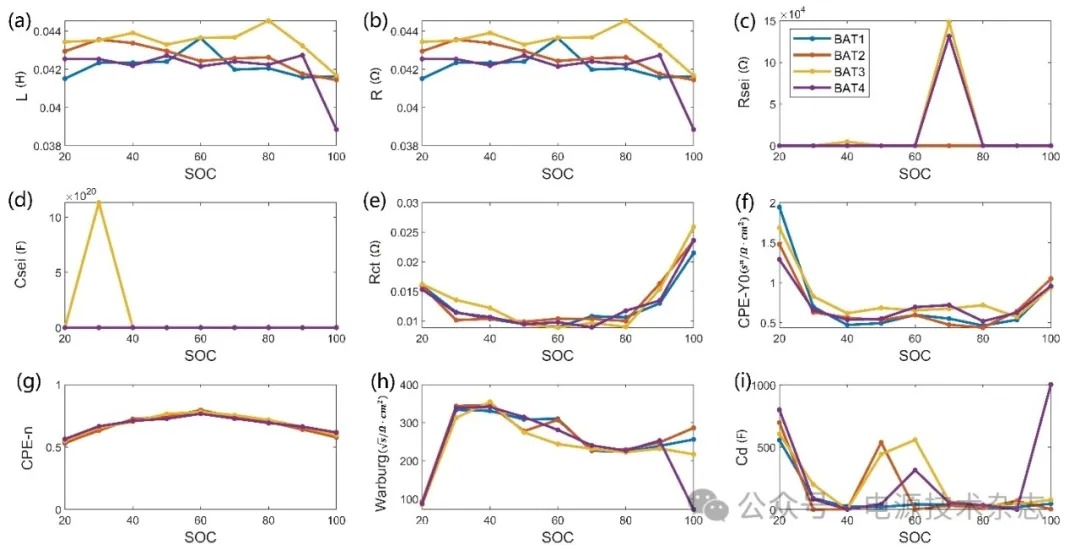
(a)电感L，（b）电池内阻R，（c）SEI膜电阻RSEI，（d）SEI膜电容CSEI，（e）电荷转移电阻Rct，（f）恒相位元件第一个参数CPE-Y0，（g）恒相位元件第二个参数CPE-n，（h）扩散阻抗Warburg，（i）扩散容抗Cd

图9 改进后的九个模型参数随电池SOC的变化趋势

4.2 SOC估计

从图9中可以看到，当电池SOC低于60%时，CPE-n随着SOC的增加而增加；而当电池的SOC高于60%时，CPE-n随着SOC的增加而降低。因此可以将电池SOC随CPE-n的变化趋势分为高于和低于60% SOC两个部分，以CPE-n为自变量，SOC为因变量，通过函数拟合两者之间的关系。

图10中给出了BAT1的SOC随CPE-n的变化关系，其中左边为电池SOC在20%～60%区间内其随参数CPE-n的变化趋势，右边则为电池SOC在60%～100%区间内其随参数CPE-n的变化趋势。从图中可以看到，电池SOC和参数CPE-n之间近似为二次函数关系，所以使用二次函数来拟合两者之间的关系。设电池SOC和参数CPE-n之间的关系为：

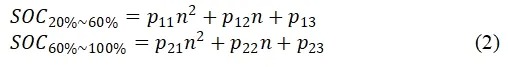
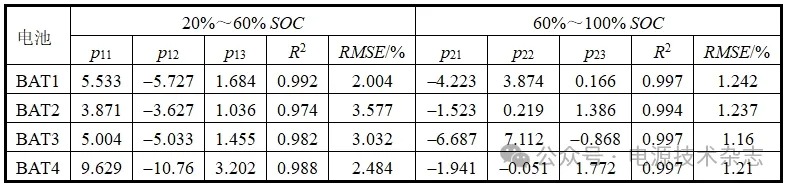
式中：p11～p23为待定系数；n为参数CPE-n。通过拟合SOC和CPE-n即可得到四颗电池的SOC和CPE-n的关系式中的待定系数。表3中给出了拟合得到的关系式的决定系数及其与实测数据之间的误差。从拟合结果中可以看到，拟合关系式的决定系数均在0.97以上，均方根误差均在3.6%以内。绝大部分的决定系数更是在0.985以上，均方根误差都在2.5%以内。特别是在60%～100% SOC段，决定系数均高于0.99，估计误差均低于1.3%。这表明使用电池内部非线性程度对其SOC进行估计是一种可行的方法。

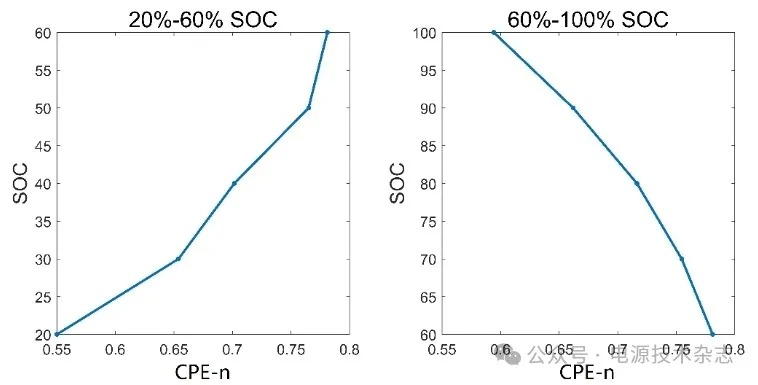
图10 BAT1电池SOC随参数CPE-n的变化趋势

表3 拟合相关系数及误差

5 结论

本文对基于EIS数据和ECM对电池的SOC估计方法进行了研究，为了获得更好拟合效果的ECM，本文对常用的ECM中的拟合效果最好的一个模型进行了改进，使其拟合精度进一步降低。为了克服传统的通过电化学工作站获取EIS数据的方式难以实际应用的问题，本文使用了更具应用潜力的阻抗测量板获得电池的EIS数据。在数据质量不高的情况下仍然能通过参数辨识从ECM参数中找到和电池SOC高度相关的参数，在保证SOC估计精度的同时实现了一条更具实用价值的基于EIS数据估计电池SOC的新途径。基于本文所提出的方法，可以在电池停止充放电后静置一段时间对其进行阻抗测量和参数辨识，并根据辨识得到的非线性参数CPE-n对其SOC进行标定，以满足常用的用以估计电池SOC的安时积分法需要每隔一段时间对电池SOC进行标定以消除累积误差的需求。